Nasa Tournament Lab - Longeron Challenge: 17th place

Introduction

On 16 January 2013, I received an email from TopCoder announcing a challenge by NASA to optimize the energy production of the International Space Station.

Here is the small teaser NASA published on youtube:

I will try to summarize the problem, but if you want to learn more on the subject, I suggest you to take a look at the Problem Statement.

Being a big fan of space related themes and as I was familiarized with TopCoder marathon challenge, I decided to dive in.

Problem summary

The goal of the contest was to maximize the solar energy production of the International Space Station for a total period (92 minute) in difficult orbital situations.

Here is a small labelled drawing I completed:

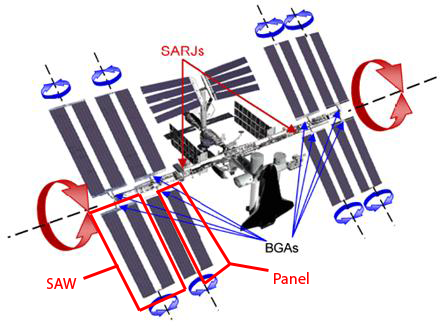
For achieving this goal, we could affect 21 parameters:

• The Yaw of the ISS, which was defined as its orientation. The orientation could only be set at the begining.
• For each minute (0 - 91), the rotation and velocity of the two Solar Alpha Rotary Joints (SARJ). These joints were moving 4 Solar Array Wings (SAW) at once.
• For each minute (0 - 91), the rotation and velocity of the 8 Beta Gimbal Assemblies (BGA). These joints were only moving 1 Solar Array Wings (SAW).

We had some constaints though:

• As presented on the video, there had to be an even number of illuminated longeron for each SAW most of the time ; there was some tolerance though (it could be illuminated on odd longeron for 21 consecutives minutes without causing any structural damage).
• There was constraints on SARJ and BGA speed and acceleration.
• Score was reduced if total amount of BGA rotation in one complete period exceeded 80 degrees.
• Score was reduced if SAW didn't meet a minimal energy production specific amount.

Problem was therefore very complex, with various parameters to take into account. Hopefully, the contest provided us a previsualizer which has been of great help for me:

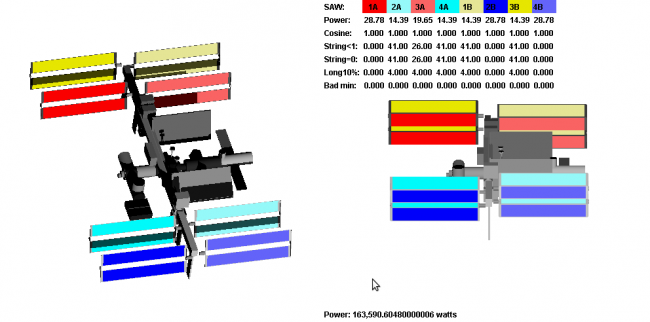
Last but not least, the solutions would be tested on 6 specific and announced orbital situations, which allowed precalculation. This way you could predetermine all angles / velocities before and submit a solution containing these values and a loop iterating on it. Most competitors, as myself, adopted this solution.

Problem analysis

This was an energy optimization problem, where time had a very importance place : at every minute, the sun position in relation to the ISS was a little bit different than the previous minute. It was important to adjust the all angles so that:

• Angle between sun rays and solar pannels had to be as near as possible to 90 degrees.
• If a panel was shadowed on more than 20% of its area, it didn't produce any energy. We had therefore to minimize shadow, and it could affect BGA angles (one SAW always shade the one just behind it), and it could affect SARJ angles (crossing angles could make one side shade the other).
• It respected maximum velocities and acceleration.

I decided that problem was complicated enough for starters, and I would better comprehend others constraints (longerons, maximum rotation of BGA...) once I had resolved this problem first.

Reducing the problem to SARJ angles

Ok, there was a lot of back and forth on this matter, I made adjustements when I implemented and tested my solution, but for clarity reason I will sumarize everything here.

So first I noticed there was a lot of parameters. Even if I moved aside Yaw angle and velocities (which could be deduced later from angles), I had still 10 angles to determine every minute. All those angles could be between 0 and 360 degrees, so it was impossible de test all values.

As I noticed before, angle between sun rays and solar pannels had to be as near as possible to 90 degrees. This was a start: if I didn't take into account pannel shadows and always set this angle to 90 degrees, I didn't have to worry about BGA angle and had to manage only the two SARJ angles, which was much more easy.

For the simplest orbital positions (for those who have read the problem statement, I am talking about beta angle -71 and 71), this simple supposition worked.

I noticed though that SAWs always shade one pane of the SAW behind it. No matter how you set the angle, you could never get a better solution than this. I think this is simply not possible, as none of the other participants succeeded to.

But my first supposition was not sufficient for other orbital positions.

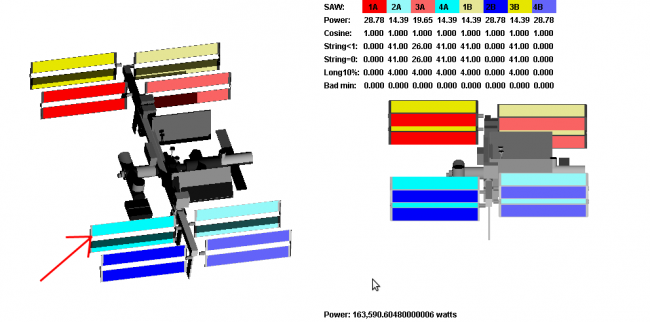
ISS on simplest orbital position with first solution: no shadow

ISS on more complicated orbital position with first solution: shadow

With this image we clearly see that we need to change the front SAW angles. I first tried to solve this problem with geometry. This is a line-circle intersection problem ; the circle represented by all position front SAW can have, and the line is the sun ray intersecting the back SAW panel bottom. But when testing on the visualizer I noticed there was some small difference I didn't succeed to explain. So instead I solved this matter with a linear regression.

This second solution was sufficient enough for most orbital position, except for two (for those who have read the problem statement, I am talking about beta angle -73 and 73). For those solutions, I noticed total amount of BGA angles rotation exceeded a lot the limit of 80 degrees. After some testing, I determined two solution to this problem:

• limit SARJ angles variation (especialy going back and forth)
• apply a lower bound for BGA angles in order to limit there variation. If the lower bound was near enough 90 degrees, there wasn't so much loss, but it was preventing most variation (this can be explained with line-circle problem).

SARJ angles strategy

Automatic path calculation ?

Once I reduced the problem to the management of two SARJ angles, the problem was less complicated. The idea was to be able to plan the best path those rotation could take on the 92 minutes. But I had three problems :

• I had to know the power generated on a given state (orbital position + angles the program chosed). The vizualizer provided a way to get this value on one state, but this took time (on my computer, one test case took about 80ms to be calculated)
• Angles were real numbers, so even with only two angles to determine there was an infinite number of possible positions.
• My knowledge on this domain was very limited

I know now I made a mistake, but back then I decided that, since there was going to be a lot of test cases, I had to boost the calculation time, and the only way to do that was a linear regression on SARJ angles and BGA angles. I was wrong, because:

• Using BGA angles complexified a lot the problem and, as I wrote on previous part, it was possible to determine optimal BGA angles by calculation. But what you read was my final solution and I didn't have all the clues back then.
• Even without the first mistake, I suspect the results would not be conclusive since there would still be a lot of angles, on a lot of different situation.

So when I did the linear regression on 10 million random "possible" states, results were very disappointing : there was a mean variation of 20% between the real value and the value calculated by linear regression.

I was stuck, and I didn't have a lot of time remaining. Fortunatly, I came up with a new solution, which I agree could seem a little bit eccentric, but at the end turned out pretty well.

Manually determine the path with an human interface

As I wrote before, our submission would be tested on only 6 differents and announced orbital positions. 6 is not a big number, and since those positions were already announced, it appeared it was clearly possible to determine them manually with a human interface.

By manually setting them, I could understand what strategy I could adopt, and if I had enough time, I could come up with an algorithm based on my observations. In fact, I didn't have the time to implement the algorithm for processing the SARJ angles strategy, but it helped me a lot for BGA angles.

This supposed that the time needed for one path, that is setting 2 * 92 = 184 angles, would not take too much time to manually configure. This was the challenge of the interface.

Interface implementation

The idea was to make an easy interface in order to manually configure path very quickly. I gradually added new features as I needed them, but this is what it looked like at the end:

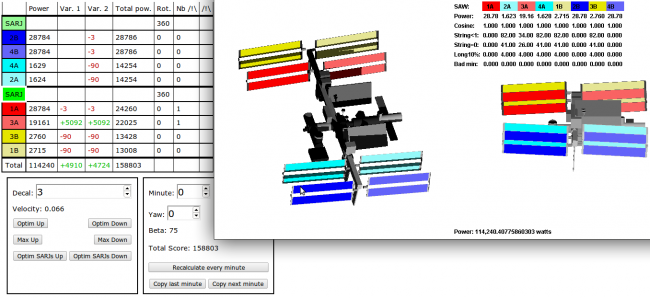
I used my interface near the vizualizer in order to get an idea of the current state

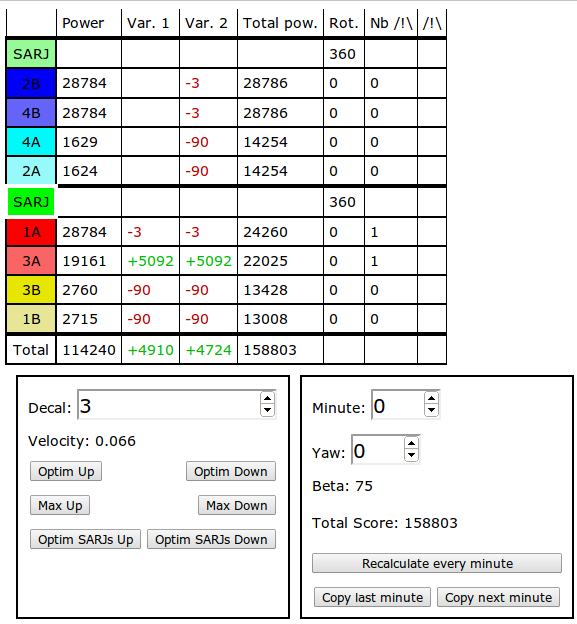
Here, a larger snapshot on the interface

That's basically with this interface that I solved the problem. The vizualizer supplied me a preview of the current state, and that was very important in order to understand which area were shadowed and optimize the score this way.

On my interface, first, you can see a table on the top.

This table has 12 lines: first for header, then one for each SARJ and linked SAWs, and the last line is the total (sum of powers...).

This table has 8 columns:

• Angle: by clicking on a line, I selected an angle (I could choose BGA as SARJ angles) and then I was able to modify its angle with the lower interface.
• Power: power generated by the item on current minute.
• Var. 1: power variation since I selected last angle.
• Var. 2: power variation since I changed minute.
• Total pow.: total power produced on the whole orbit.
• Rot.: total item rotation (in order to see If I didn't exceed the 80 degrees limitation for BGAs)
• NB /!\: total longeron bad score for the whole orbit
• /!\: are the longeron dangerous on this orbit

The interface has then 2 lower rectangle.

The first rectangle allows to change the selected angle.

• The number input allowed me to change angle difference with the "obvious optimal angle", that is the angle which would produce the most power if station and station side weren't shadowing each other. On optimal cases this difference was near from 0 that allowed me to reduce angle search.
• The two second line buttons allowed me to search a near local optimum for the angle. It proved to be very useful, because I quickly noticed that SARJs were often stuck for few minutes on a given position since if it moved forward it was shadowed by a space station component.
• The two third line buttons allowed me to set the angle to a minimum or maximum considering velocity and acceleration constraint. These two turned out not very useful.
• The objective of the two last buttons allowed me to the two optimal angles when one was shading the other. I didn't use it very often.

The second rectangle allowed to control the state:

• On first line you could change current minute.
• On second line you could change the Yaw and notice if there was any improvement.
• Third line: current beta.
• Fourth line: total score (with minimum energy production and angle variation malus)
• Fifth line button allowed me to refresh every minute when I changed the Yaw.
• And the 6th line buttons allowed me to copy last or next minute state, because I noticed that from one minute to the next angle variation wasn't very important.

Results

Time was very short and I finished my sixth case one hour before the end. So I submitted my program with those values manually configured.

Few days later, score came back, and it turned out pretty well: my solution appeared on the 17th place on over 4000 subscribers and more than 400 submitted solution. Here are the standings and the forums where a lot of interesting ideas were discussed.

Here is a small preview of my solution for the test case beta = 71° (running on two orbits):